Big O 표기법

[알고리즘] 시간 복잡도와 Big O 표기법

 Big O 표기법

 

알고리즘의 효율에서 가장 중요한 부분은 ‘n이 커질 때 알고리즘의 단계가 얼마만큼 증가하는가’이고, 이것을 잘 나타내는 빅 O 표기법을 사용합니다.

 

빅 O 표기법은 점근 표기법(Asymptotic Notation) 중 하나인데, 점근 표기법이란 ‘점근(漸近): 차츰 점, 가까울 근’이라는 이름에서 알 수 있듯이 알고리즘의 수행 시간을 대략적으로 나타내는 방법을 말합니다. 여기서 말한 ‘대략적으로’는 ‘정확하게’의 반대말이 아니라 ‘자세하게’의 반대말입니다.

 

소규모 데이터를 다루는 경우 우수한 성능의 알고리즘과 그렇지 않은 알고리즘 사이에 차이가 거의 없습니다. 퀵 정렬이 훨씬 우수한 성능을 갖고 있지만, 오히려 소규모 데이터를 정렬할 때에는 삽입 정렬을 사용하는 편이 더 나은 효율을 보이죠. 알고리즘 성능 차이는 대규모 데이터를 다룰 때 두드러집니다. 그 규모가 무한대에 가까워진다면 그 차이는 아주 분명해지겠죠.

 

대표적으로 사용하는 점근 표기법은 다음 3가지입니다.

• O(Big O) 표기법: 알고리즘 성능이 최악인 경우(수행 시간의 상한)를 나타낼 때 사용
• Ω(Big Omega) 표기법:  알고리즘의 성능이 최선인 경우(수행 시간의 하한)를 나타낼 때 사용
• Θ(Big Theta) 표기법: 알고리즘이 처리해야 하는 수행 시간의 상한과 하한을 동시에 나타냄

 

빅 O 표기법은 최악의 경우 알고리즘 수행 시간을 나타냅니다. 다시 말해 알고리즘을 사용하는 어떤 경우에도 보장되는 알고리즘의 성능이라고 할 수 있습니다. 최악의 경우에 대한 알고리즘 수행 시간이 가장 쓸모가 많다 보니 가장 많이 사용하는 알고리즘 성능 표기법으로 빅 O 표기법이 꼽히곤 합니다.

 

빅 O 표기법을 사용하는 방법은 대문자 O를 쓰고 그 옆에 괄호를 열고 닫은 후 그 안에 증가 함수를 넣습니다. 증가 함수는 입력 데이터의 크기 n에 대해 알고리즘의 수행 시간이 늘어나는 비율을 나타내는 함수입니다.

 

 

 

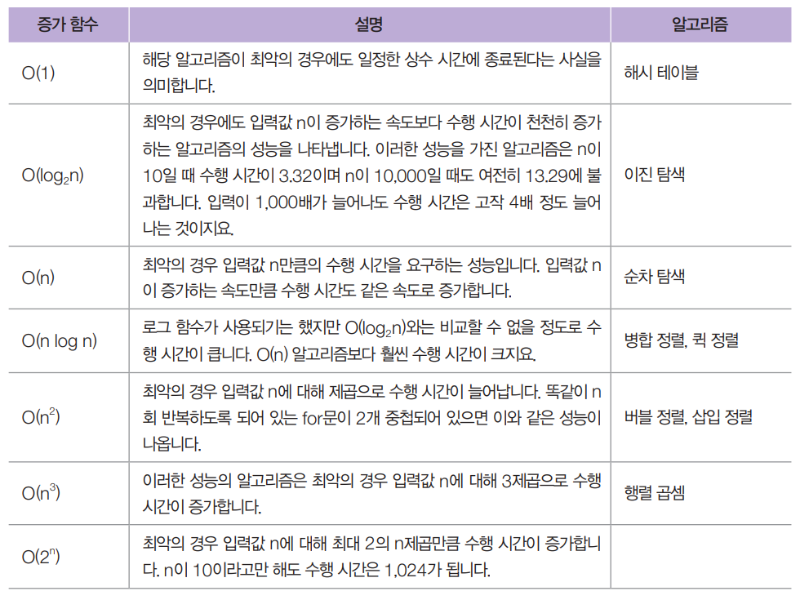
1. O(1)ex) stack의 push, pop
2. 입력값(N)이 증가해도 실행시간은 동일한 알고리즘, index로 접근하여 바로 처리할 수 있는 연산 과정의 시간 복잡도 → 기본 연산 수라고 생각하면 편함
3. O(log N)ex) binary search 알고리즘, tree 형태 자료구조 탐색
4. 연산이 한 번 실행될 때 마다 데이터의 크기가 절반 감소하는 알고리즘 (log의 지수는 항상 2)
5. O(N)ex) 1중 for문
6. 입력값(N)이 증가함에 따라 실행시간도 선형적으로 증가하는 알고리즘
7. O(N log N)ex) 퀵 / 병합 / 힙 정렬
8. O(N)의 알고리즘과 O(log N)의 알고리즘이 중첩된 형태
9. O(N^2)ex) 2중 For 문, 삽입/버블/선택 정렬
10. O(N)의 알고리즘과 O(log N)의 알고리즘이 중첩된 형태
11. O(2^N)ex) fibonacci 수열
12. 빅오 표기법 중 가장 느린 시간 복잡도로 주로 재귀적으로 수행하는 알고리즘이 이에 해당