개발자공부일기
Array과 LinkedList 본문
배열(Array)이란?
배열은 연속된 메모리 위치에 요소를 저장하는 데 사용되는 데이터 구조입니다. 이는 각 요소가 서로 인접한 메모리 위치에 저장된다는 것을 의미합니다. 또한 배열의 크기는 변경할 수 없으며 미리 선언됩니다.

이것은 각 상자가 인접한 메모리 위치에 해당하는 크기 6 의 배열의 예입니다 . 보시다시피, 배열은 처음에 크기 6 으로 선언되었지만 인덱스 0-4 만 사용됩니다. 그러나 인덱스 5 가 비어 있고 값이 없지만 메모리 공간을 차지하고 있습니다.
접근
요소에 접근할 때 배열은 매우 효율적이며 상수 시간 O(1)이 걸립니다 .
이는 각 메모리 위치의 순차적 특성 때문입니다. 예를 들어 인덱스 4에서 요소를 검색하고 싶다고 가정해 보겠습니다. 그런 다음 배열의 기본 주소(첫 번째 요소의 메모리 주소)를 사용하여 간단한 산술 연산으로 인덱스의 메모리 주소를 추론할 수 있습니다.

삽입
배열에 요소를 삽입하는 데는 평균 O(n) 의 시간 복잡도가 사용됩니다 .
이는 배열의 시작 부분에 요소를 삽입하면 전체 배열이 오른쪽으로 한 칸 이동해야 하므로 최악의 시간 복잡도가 O(n) 이기 때문입니다 .

그러나 배열의 끝에 요소 5를 추가하려는 경우 아무 요소도 이동할 필요가 없으므로 O(1)의 최적 시간 복잡도가 되어 쉽습니다 .
하지만 이것은 매우 특별한 경우일 뿐이며, 실제로는 모든 위치에 요소가 삽입되고 평균 인덱스는 0.5n 입니다. 따라서 이동이 필요한 요소의 수는 n 에 비례하여 총 평균 시간 복잡도가 O(n)이 된다는 결론을 내리는 것이 정확합니다 .
배열의 메모리 효율성
배열은 데이터를 저장할 때 상당히 메모리 효율적입니다. 그러나 배열의 크기를 선언해야 하기 때문에 크기가 너무 커질 가능성이 있습니다.
예를 들어 이전의 예를 살펴보겠습니다.

크기가 6인 이 배열에서 5개의 메모리 주소만 유용 하게 사용되고 있으며, 마지막 메모리 주소 105는 공간 낭비 로 작용합니다 . 이러한 유형의 발생은 특히 동적 데이터를 처리할 때 배열에서 흔히 발생하며 Linked List에서는 발생하지 않는 문제입니다.
연결 리스트(Linked List)란?
배열과 달리 Linked List 는 연속된 메모리 위치에 요소를 저장하지 않고 대신 포인터를 사용하여 다음 요소의 메모리 주소를 저장합니다. Linked List 는 4가지 기본 특성으로 구성됩니다.
- Head: 첫 번째 요소의 메모리 주소를 저장하는 포인터.
- Data: 이는 요소의 값을 저장합니다.
- Next/Link: 다음 요소의 메모리 주소를 가리키는 포인터입니다.
- Node: 이는 데이터와 링크의 총칭입니다.
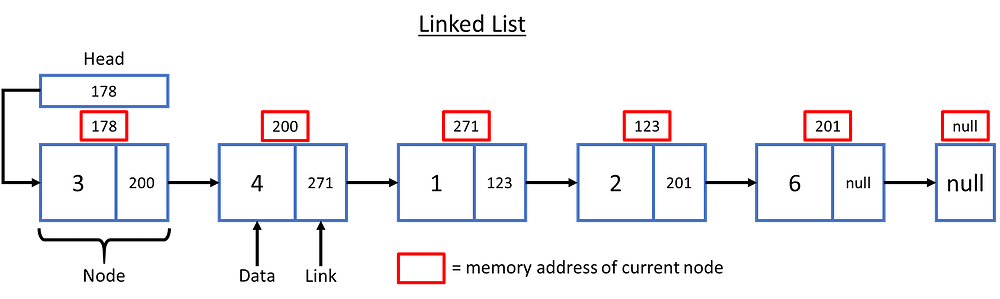
작동 원리
- 먼저 Head는 첫 번째 노드의 메모리 주소를 가리킵니다. 이 노드는 데이터 값과 다음 노드를 가리키는 포인터인 링크를 포함하고 있습니다.
- 다음 노드는 두 번째 요소의 데이터 값과 세 번째 노드의 메모리 주소를 가리키는 링크를 보유합니다.
- 마지막 노드까지 이런 과정이 계속됩니다.
- 마지막 노드에서는 더 이상 이어지는 노드가 없으므로 링크는 null을 가리킵니다.
접근
연속적인 배열의 특성으로 인해 액세스가 매우 빠릅니다. 그러나 Linked List의 경우 주어진 인덱스의 메모리 주소를 간단한 산술로 알 수 없습니다.
요소에 접근하기 위해 컴퓨터는 헤드 포인터에서 시작하여 원하는 인덱스에 도달할 때까지 각 노드의 포인터를 따라가야 합니다. 따라서 접근은 Linked List 의 크기에 정비례합니다.
최상의 시간 복잡도는 시작 요소에 액세스하는 경우 상수 시간 O(1) 이고 최악의 시간 복잡도는 연결 목록의 마지막 요소에 액세스하는 경우 O(n) 입니다 . 전반적으로 평균 시간 복잡도는 액세스되는 평균 인덱스가 n/2 이므로 O(n) 입니다 .
삽입
Linked List 에 요소를 삽입하는 것은 배열보다 효율적이며 조작이 덜 필요합니다. 이는 포인터 형식 때문일 수 있습니다.
Linked List 에 새로운 요소를 삽입할 때, 이전 노드의 포인터는 새로 추가된 노드의 주소로 변경되어야 합니다. 그러나 그 위치에 도달하려면 먼저 Linked List 를 원하는 삽입 인덱스까지 탐색해야 하므로 평균 O(n) 시간이 걸립니다 .

이 예에서, 새로운 노드가 Linked List 의 중간에 삽입되고 있습니다. 보시다시피, 이전 노드의 포인터가 새로운 노드를 저장하기 위해 변경되었습니다.
마찬가지로 Linked List 의 시작 부분에 새 노드가 삽입되면 헤드 포인터가 대체되어 새 시작 노드의 메모리 주소를 가리키게 됩니다. 이로 인해 O(1)의 최적 시간 복잡도가 발생합니다 .
Linked List 의 메모리 효율성
배열은 데이터 값만 저장하면 되는 반면, Linked List 는 데이터 값뿐만 아니라 각 포인터에 저장된 메모리 주소도 저장해야 합니다. 이렇게 하면 전체 메모리 사용량이 늘어나지만, 배열과는 달리 크기가 동적이므로 모든 메모리가 유용하고 사용되지 않는 메모리가 없습니다.
정리
배열에 비해 Linked List의 장점:
- 효율적인 삽입 및 삭제 . : 중간에 항목을 삽입(또는 삭제)하기 위해 몇 개의 포인터(또는 참조)만 변경하면 됩니다. 연결 리스트의 어느 지점에서든 삽입 및 삭제는 O(1) 시간이 걸립니다. 반면 배열 데이터 구조에서는 중간에 삽입/삭제는 O(n) 시간이 걸립니다.
- Queue와 Deque 구현 : 간단한 배열 구현은 전혀 효율적이지 않습니다. 효율적으로 구현하려면 복잡한 원형 배열을 사용해야 합니다. 하지만 연결 리스트를 사용하면 쉽고 간단합니다. 그래서 대부분의 언어 라이브러리는 이러한 데이터 구조를 구현하기 위해 내부적으로 연결 리스트를 사용합니다.
- 어떤 경우에는 공간 효율적: 연결 리스트는 미리 요소의 수를 추측할 수 없는 경우 배열에 비해 공간 효율적일 수 있습니다. 배열의 경우 항목에 대한 전체 메모리가 함께 할당됩니다. C++의 벡터나 Python의 리스트 또는 Java의 ArrayList와 같은 동적 크기 배열의 경우에도 내부 작업에는 현재 용량을 초과하여 삽입이 발생할 때 전체 메모리의 할당 해제와 더 큰 청크 할당이 포함됩니다.
- 삭제/추가가 가능한 원형 리스트: 원형 연결 리스트는 순환 방식으로 삭제/삽입을 빠르게 수행할 수 있기 때문에 실제 세계에서 CPU 라운드 로빈 스케줄링이나 비슷한 요구 사항을 구현하는 데 유용합니다.
Linked List에 비해 배열의 장점:
- 임의 접근 . : O(1) 시간 안에 i번째 항목에 접근할 수 있습니다(기본 산술만 필요함, 기본 주소 사용). 연결 리스트의 경우 순차 접근으로 인해 O(n) 연산입니다 .
- 캐시 친화성 : 배열 항목(또는 항목 참조)은 인접한 위치에 저장되므로 배열 캐시에 친화적입니다
- 사용이 쉬움: 배열은 비교적 사용하기 쉽고 프로그래밍 언어의 핵심으로 사용할 수 있습니다.
- 오버헤드 감소: 연결 리스트와 달리, 모든 항목에 추가 참조/포인터를 저장할 필요가 없습니다.
.
'CS지식 > 자료구조' 카테고리의 다른 글
| Red-Black Tree (0) | 2025.03.05 |
|---|---|
| B+ Tree (0) | 2025.03.04 |
| 이진트리, 이진 검색트리, 힙 (0) | 2025.03.03 |
| 그래프(Graph)와 트리(Tree) (0) | 2025.02.21 |
| Stack과 Queue (0) | 2025.02.17 |




